RLHF Suppresses Reasoning and Elections Are To Blame

This post is based on Zhao, Dai & Awasthi 2025 [1].

RLHF is good at some things, like instruction tuning, but is also known to suppress reasoning capabilities. It's now common to blame this on the RLHF algorithm: because RLHF collects preference data in a separate stage from training, reliance on offline data results in overfitting/reward-hacking and necessitates aggressive regularization (hence the saying "RLHF isn't real RL").

But we've recently found that there's another, orthogonal, and more troubling explanation: the use of preferences as a data modality results in information loss that unavoidably suppresses "robust behaviors" (such as backtracking) and, by extension, suppresses reasoning. As a fundamental limitation of preference data, this can't be overcome just by collecting data online or modifying the RLHF algorithm. Interestingly, the principles behind this impossibility result are also the same principles that tell us that elections will inevitably suppress "compromise candidates": candidates that are not usually a favorite but are a reasonable compromise for most voters. This blog is just aimed at explaining the main intuition behind this result; see [1] for details.

Why We Care About Preference Data

RLHF is still the dominant paradigm for instruction tuning, safety training, and alignment. There's a good reason for this: preference data is the most convenient way of getting human feedback. Because humans can usually pick between options faster than they can score them, preferences are cheaper to collect and typically less noisy than human-labeled SFT or reward data. Preference data also has the advantage of capturing fine-grained signals, e.g. distinguishing between two potential responses even when one is only a tiny bit better than the other—these signals would otherwise be drowned out in noise.

Yet the greatest recent advancements in reasoning capabilities (e.g., o1, r1) have come from reinforcement learning with verifiable rewards (RLVR). Part of this is due to supply: answers to reasoning tasks can often be verified programatically. But while relying on verification rewards works fine for coding and close-ended exams, human feedback is still needed for many reasoning-heavy tasks like writing 📝, code completion 🤖, agentic research 🔎, and trip planning ✈️. Indeed, there certainly have been attempts to imbue reasoning with RLHF, primarily for code completion and writing tasks, though primarily within larger companies and with less public visibility.

Unfortunately, it seems that RLHF is quite poor at eliciting such capabilities. As mentioned before, this is usually attributed to the fact that RLHF depends on offline data and hence needs strong KL regularization, which in turn inhibits post-training from sufficiently updating the model's chain-of-thought behavior. But this isn't super compelling. Why is RLHF so limiting when it comes to reasoning capabilities in particular? After all, instruction-tuning also requires significant change to model behavior.

Post-Training Assigns Queries to Circuits

We're going briefly switch gears and try to think about a nice mental model for post-training. There's been a lot of recent work showing that most post-training, be it RLHF, RLVR or SFT, is primarily about rewiring how we choose which circuits (in our pretrained model) to apply to queries. For the sake of this blog, we'll just think of circuits as encoding behaviors like "use Jensen's inequality" or "make a funny pun" or "backtrack and fix our mistake".

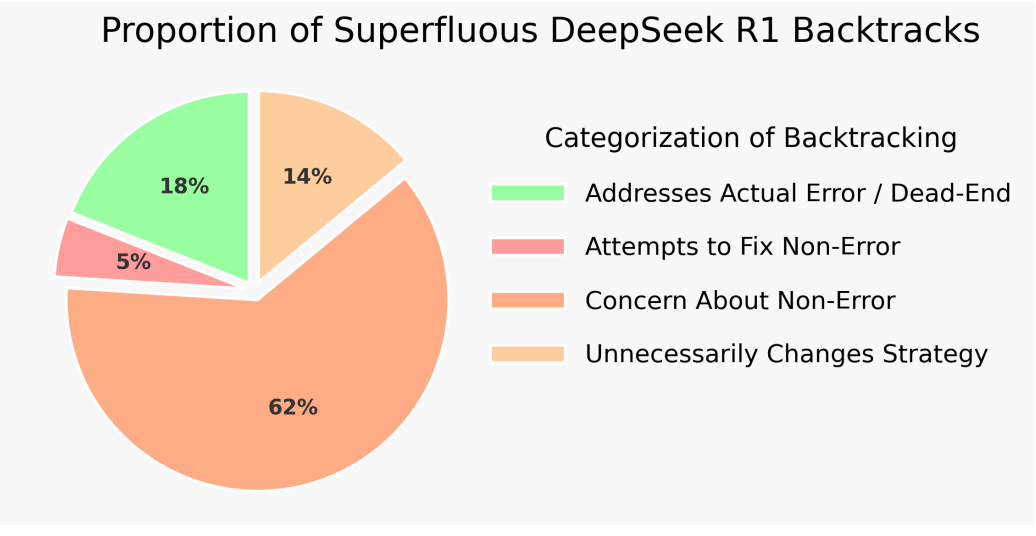
It can be quite hard to know which circuit to use when we're given a query. For example, it's hard to tell when to use a cautious back-tracking chain-of-thought versus steamrolling to an obvious answer (part of the reason for GPT5's delays). Indeed, if you look at the chains-of-thought in reasoning models, you'll see that most backtracking is unnecessary! Yet even though it's hard for these models to know when to backtrack, RL has still taught these post-trained models that even somewhat indiscriminate use of backtracking circuits is helpful, because it's better to be safe than sorry when afforded long COTs.

The Impossibility of Elections (Post-Training)

This brings us to an interesting analogy between post-training and election systems. Think of each potential query as a voter, each circuit in our pretrained model as an election candidate, and a preference learning algorithm as an election system. An election system takes in ballots telling us about each voter's preferences and uses it to pick out a good candidate. Similarly, a preference learning algorithm takes in preference data on which circuits result in better answers for each query and uses it to decide which circuits to use when answering queries.

A classic result in social choice theory is that there is no universally good election system: having voters express their opinions through ballots simply results in the loss of too much information, making it impossible to extrapolate the true social utility of each candidate. More recently, distortion theory has emerged to quantify just how much this loss of information can harm social welfare [2].

This is where the post-training analogy becomes a bit nuanced. In elections, we can't let some people have one president and others have a different president just because they disagree (I think that's just civil war). In contrast, in post-training, we aren't forced to use the same circuit to answer each query. However, as in the backtracking circuit example, we also aren't able to select the best circuit for each query—it can be hard to distinguish between queries! We can therefore still apply a pigeonhole-like argument to extend the classical impossibility results for elections to post-training. If you'll bear with a bit of math:

Basically, for any pretrained model, even if you have unlimited preference data and the preferences are collected online and without noise ^†, no matter what preference learning algorithm you use, there will always be a situation where your post-trained model ends up providing an astronomically lower utility than the best possible model you could have post-trained. In some cases, you might as well have not post-trained at all. Ouch.

Reasoning is a Compromise Candidate

A primary failure mode of (reasonable) election systems is that they suppress "compromise candidates": candidates that appeal broadly but are often not favorites. This is just because looking at ballot data alone, even if you afford yourself infinite comparisons between all possible candidates, it's impossible to tell whether a candidate is dispreferred just because they're just not great overall, or if they're not anyone's favorite but are a spectacular compromise. Because preference learning algorithms ultimately do behave like election systems, RLHF similarly ends up suppressing "compromise candidates". In the post-training context, a compromise candidate is a circuit that is not the best way to answer a query, but is a good way to answer many queries.

Unfortunately, reasoning is an exercise in robustness. Backtracking is a good example: labelers prefer when models don't need to backtrack to reach the right answer—they'd much rather a model cleanly and directly arrive at the right destination—but backtracking is still a behavior we'd like to reinforce. We actually found that it's not hard to find instances of models exhibiting reasoning behaviors like backtracking in existing RLHF datasets—they just end up being downranked even when they are otherwise satisfactory.

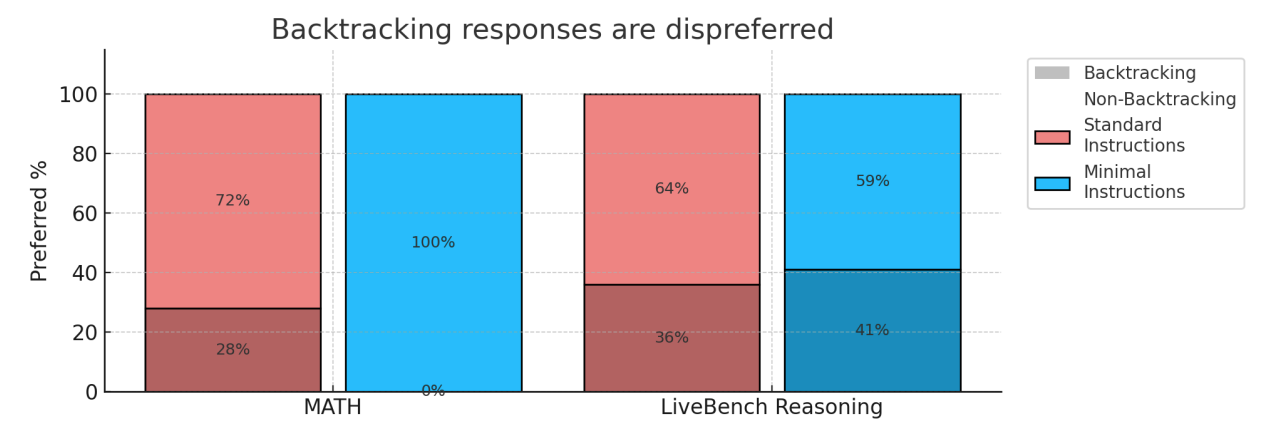
By this theory, part of the reason why RLHF is lackluster at eliciting reasoning is just that preference data itself makes it hard to reward robust strategies, and reasoning capabilities tend to correspond to robust strategies. Of course, one fix is to just to tell labelers which chain-of-thought behaviors to reward, but this is against the spirit (and original purpose) of reinforcement learning which is to optimize rewards and have models learn the best way to do things.

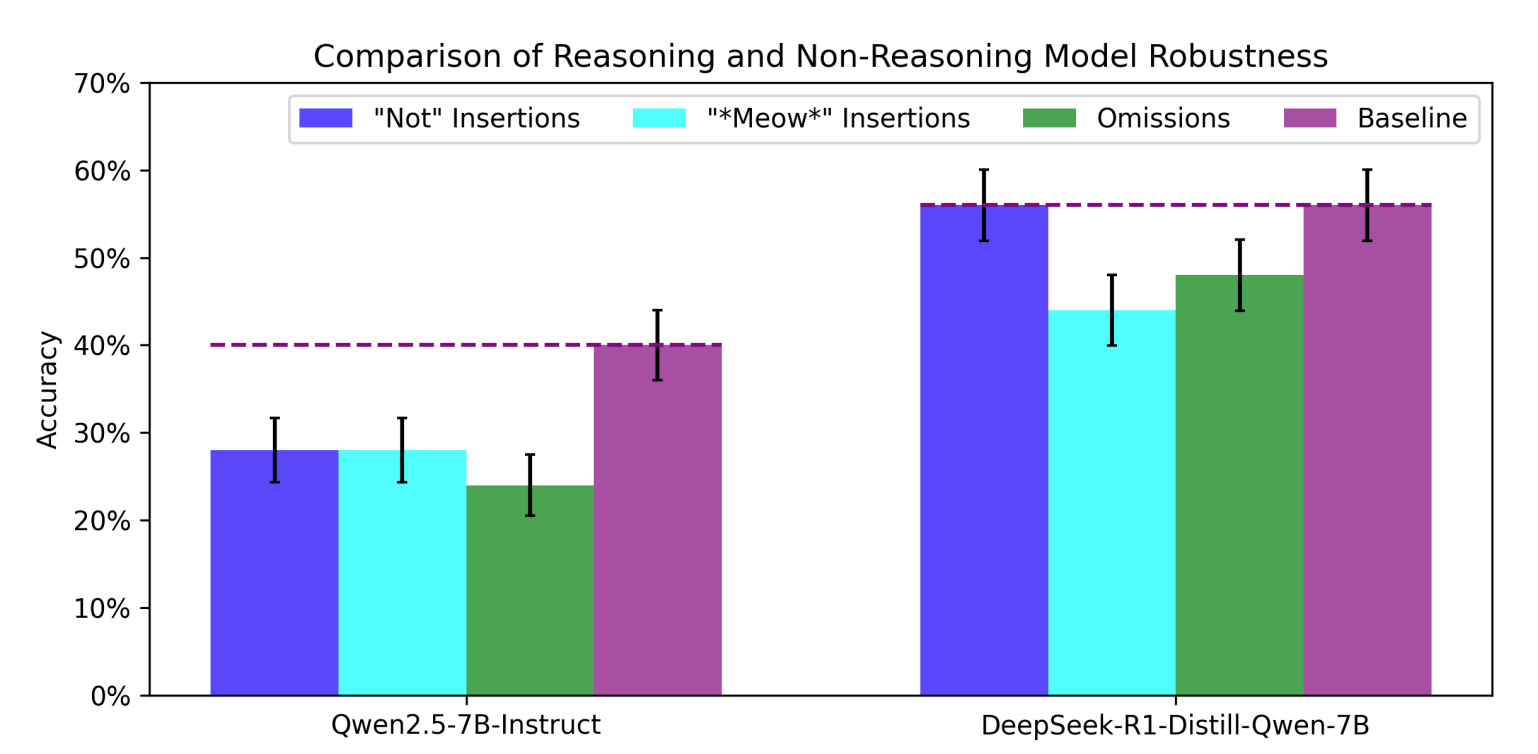
Funnily enough, the relationship between robustness and reasoning goes the other direction as well. For example, we played around with having reasoning and non-reasoning models answer math questions while actively perturbing their chains-of-thought, such as forcing them to intermittently Meow 🐈 (i.e., generate "Meow" tokens). Reasoning models are consistently more robust to these perturbations. It's been previously observed that reasoning models are more robust to adversarially written user prompts, but this form of robustness to chain-of-thought perturbations was quite surprising. To us, it's indicative of a deeper relationship between reasoning and robustness.

^† There's some nuance here where noise can sometimes help. However, even if your noise exactly follows a nice Bradley-Terry model, the same impossibility result remains. We'll defer this discussion to the paper.

References

1. Zhao, E., Dai, J., & Awasthi, P. (2025). The Limits of Preference Data for Post‑Training. Link
2. Procaccia, A., & Rosenschein, J. (2006). The distortion of cardinal preferences in voting.

Anonymous feedback welcomed here.